[Appendix E — Power Analysis]{#sec-sm-power-analysis .quarto-section-identifier}

doi:10.17605/OSF.IO/S4TBZ

Appendix E — Power Analysis

E.1 Overview

This document presents a power analysis for the Minimal Effect Size (MES) considered in the hypothesis test.

For an in-depth discussion of the thesis methods, see Supplementary Material B.

E.2 Setting the Environment

Code

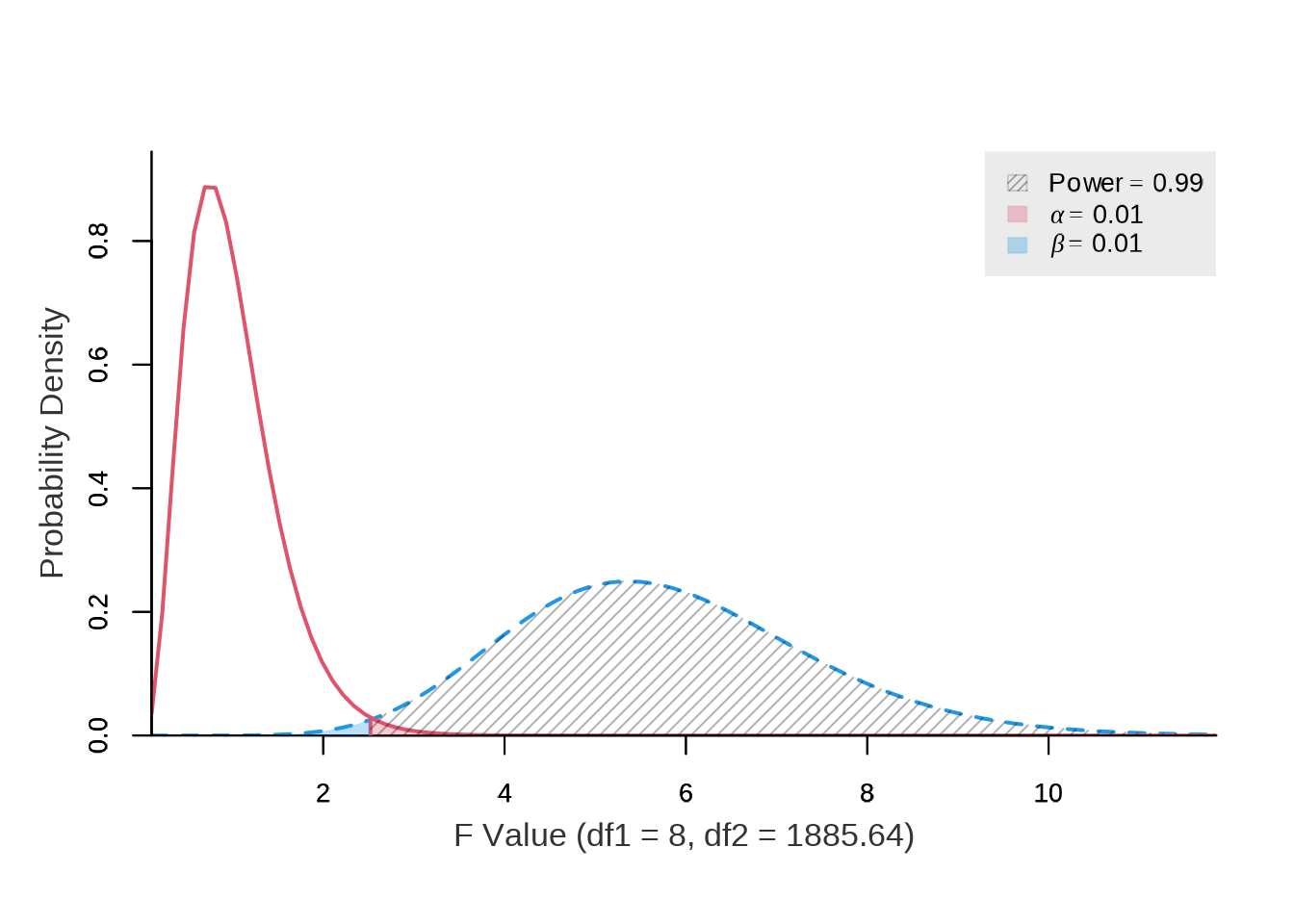
library(pwrss)

E.3 Hypothesis Test A

The results indicate that at least \(1,895\) observations per variable are required to achieve a power of \(0.99\) (\(1 - \beta\)) and a significance level (\(\alpha\)) of \(0.01\) for the Test A. The dataset contains \(65,824\) observations, which exceeds this requirement.

pwr_analysis <- pwrss::pwrss.f.reg(
  f2 = 0.02, # Minimal Effect Size (MES)
  k = 8, # Number of predictors
  power = 0.99,
  alpha = 0.01
)
#>  Linear Regression (F test) 
#>  R-squared Deviation from 0 (zero) 
#>  H0: r2 = 0 
#>  HA: r2 > 0 
#>  ------------------------------ 
#>   Statistical power = 0.99 
#>   n = 1895 
#>  ------------------------------ 
#>  Numerator degrees of freedom = 8 
#>  Denominator degrees of freedom = 1885.64 
#>  Non-centrality parameter = 37.893 
#>  Type I error rate = 0.01 
#>  Type II error rate = 0.01

Code

pwrss::power.f.test(
  ncp = pwr_analysis$ncp,
  df1 = pwr_analysis$df1,
  df2 = pwr_analysis$df2,
  alpha = pwr_analysis$parms$alpha,
  plot = TRUE
)

Figure E.1: Visual representation of the power analysis for Test A.

E.4 Hypothesis Test B

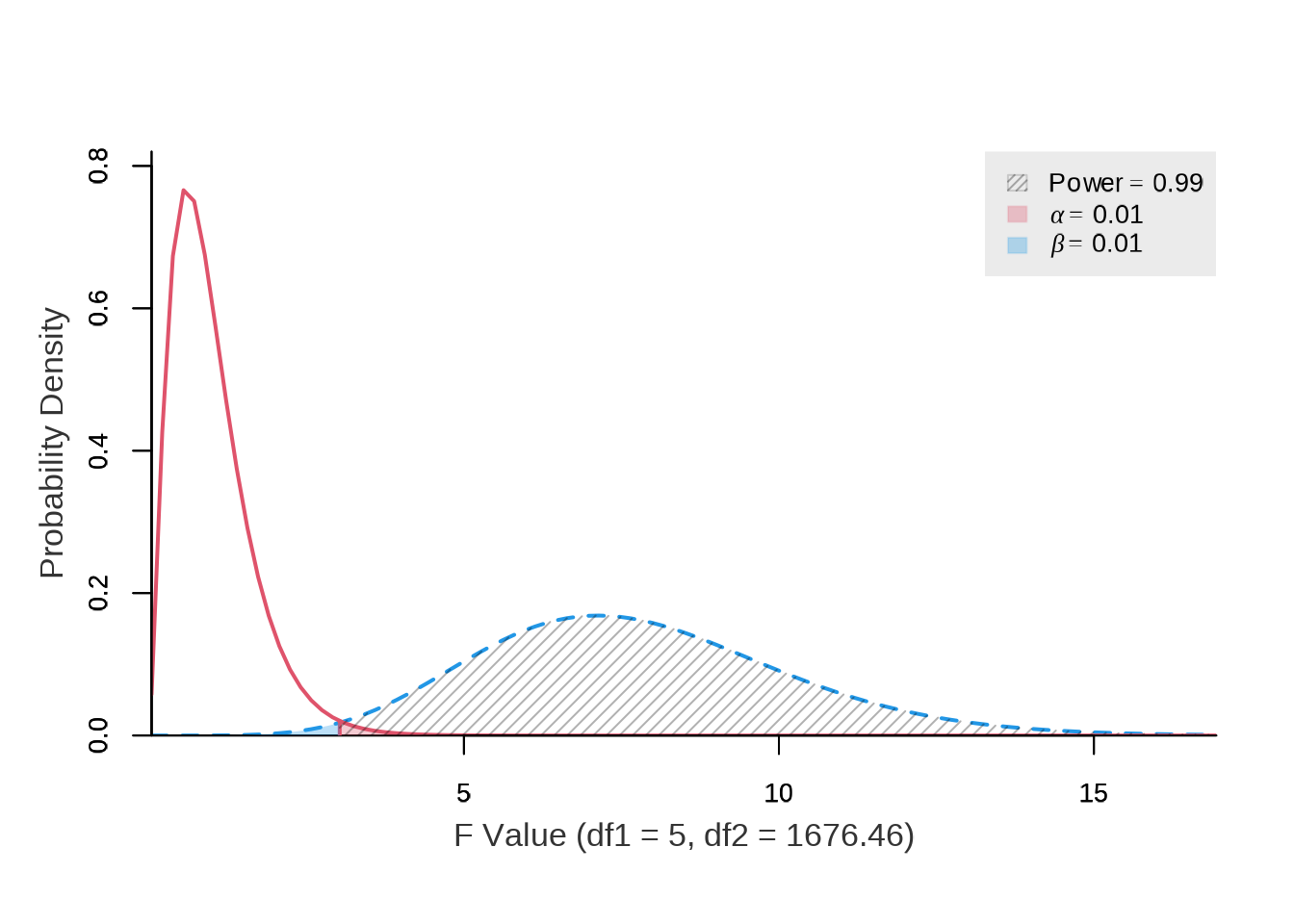
The results indicate that at least \(1,683\) observations per variable are required to achieve a power of \(0.99\) (\(1 - \beta\)) and a significance level (\(\alpha\)) of \(0.01\) for the Test B. The dataset contains \(65,824\) observations, which exceeds this requirement.

pwr_analysis <- pwrss::pwrss.f.reg(
  f2 = 0.02, # Minimal Effect Size (MES)
  k = 5, # Number of predictors
  power = 0.99,
  alpha = 0.01
)
#>  Linear Regression (F test) 
#>  R-squared Deviation from 0 (zero) 
#>  H0: r2 = 0 
#>  HA: r2 > 0 
#>  ------------------------------ 
#>   Statistical power = 0.99 
#>   n = 1683 
#>  ------------------------------ 
#>  Numerator degrees of freedom = 5 
#>  Denominator degrees of freedom = 1676.459 
#>  Non-centrality parameter = 33.649 
#>  Type I error rate = 0.01 
#>  Type II error rate = 0.01

Code

pwrss::power.f.test(
  ncp = pwr_analysis$ncp,
  df1 = pwr_analysis$df1,
  df2 = pwr_analysis$df2,
  alpha = pwr_analysis$parms$alpha,
  plot = TRUE
)

Figure E.2: Visual representation of the power analysis for Test B.