Code
library(pwrss)This document presents a power analysis for the Minimal Effect Size (MES) considered in the hypothesis test.
For an in-depth discussion of the thesis methods, see Supplementary Material B.
library(pwrss)The results indicate that at least \(1,895\) observations per variable are required to achieve a power of \(0.99\) (\(1 - \beta\)) and a significance level (\(\alpha\)) of \(0.01\) for the Test A. The dataset contains \(65,824\) observations, which exceeds this requirement.
pwr_analysis <- pwrss::pwrss.f.reg(
f2 = 0.02, # Minimal Effect Size (MES)
k = 8, # Number of predictors
power = 0.99,
alpha = 0.01
)
#> Linear Regression (F test)
#> R-squared Deviation from 0 (zero)
#> H0: r2 = 0
#> HA: r2 > 0
#> ------------------------------
#> Statistical power = 0.99
#> n = 1895
#> ------------------------------
#> Numerator degrees of freedom = 8
#> Denominator degrees of freedom = 1885.64
#> Non-centrality parameter = 37.893
#> Type I error rate = 0.01
#> Type II error rate = 0.01pwrss::power.f.test(
ncp = pwr_analysis$ncp,
df1 = pwr_analysis$df1,
df2 = pwr_analysis$df2,
alpha = pwr_analysis$parms$alpha,
plot = TRUE
)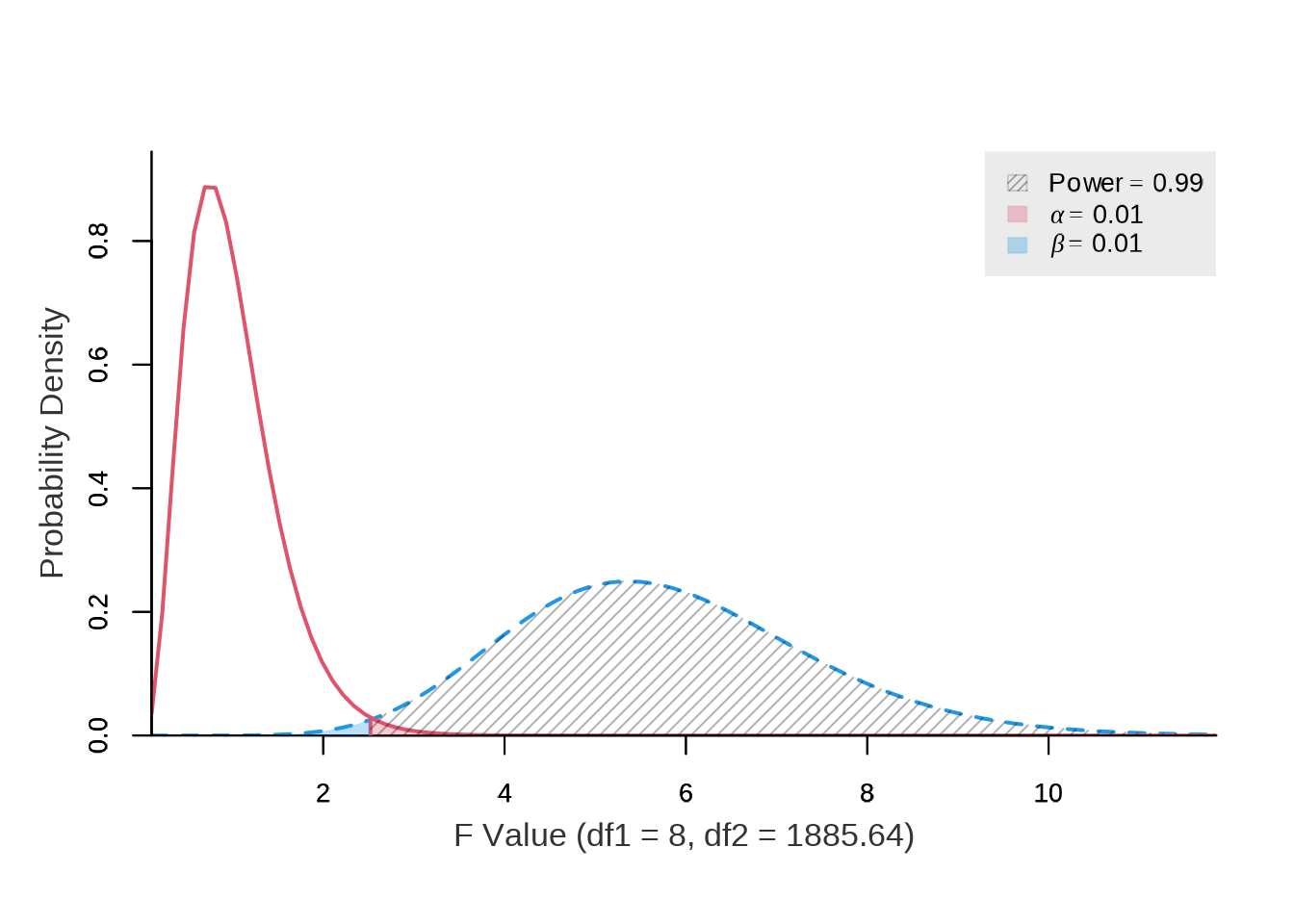
#> power ncp.alt ncp.null alpha df1 df2 f.crit
#> 0.989999999 37.893 0 0.01 8 1885.639848 2.520678643Source: Created by the author.
The results indicate that at least \(1,683\) observations per variable are required to achieve a power of \(0.99\) (\(1 - \beta\)) and a significance level (\(\alpha\)) of \(0.01\) for the Test B. The dataset contains \(65,824\) observations, which exceeds this requirement.
pwr_analysis <- pwrss::pwrss.f.reg(
f2 = 0.02, # Minimal Effect Size (MES)
k = 5, # Number of predictors
power = 0.99,
alpha = 0.01
)
#> Linear Regression (F test)
#> R-squared Deviation from 0 (zero)
#> H0: r2 = 0
#> HA: r2 > 0
#> ------------------------------
#> Statistical power = 0.99
#> n = 1683
#> ------------------------------
#> Numerator degrees of freedom = 5
#> Denominator degrees of freedom = 1676.459
#> Non-centrality parameter = 33.649
#> Type I error rate = 0.01
#> Type II error rate = 0.01pwrss::power.f.test(
ncp = pwr_analysis$ncp,
df1 = pwr_analysis$df1,
df2 = pwr_analysis$df2,
alpha = pwr_analysis$parms$alpha,
plot = TRUE
)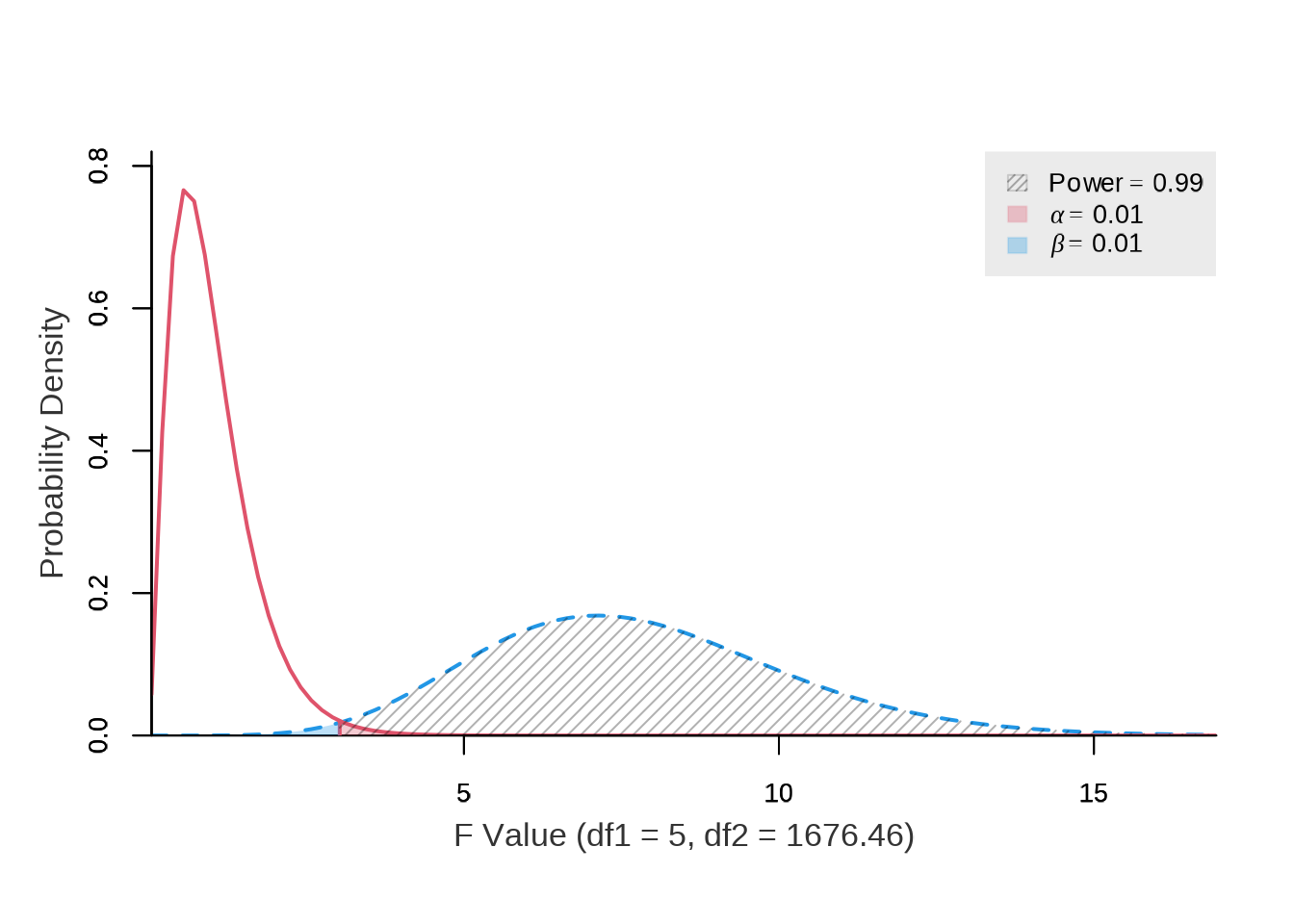
#> power ncp.alt ncp.null alpha df1 df2 f.crit
#> 0.9900000002 33.649 0 0.01 5 1676.459387 3.028152636Source: Created by the author.