Appendix E — Chapter 6 supplemental material

You are reading the work-in-progress of this thesis.

This chapter should be readable but is currently undergoing final polishing.

E.1 Hypothesis

Statement
Populations residing near the equator (latitude 0°) exhibit, on average, a shorter/morning circadian phenotype when compared to populations residing near the poles of the planet (Horzum et al., 2015; Hut et al., 2013; Leocadio-Miguel et al., 2014, 2017; Pittendrigh et al., 1991; Randler & Rahafar, 2017).

The study hypothesis was tested using nested models of multiple linear regressions. The main idea of nested models is to verify the effect of the inclusion of one or more predictors in the model variance explanation (i.e., the \(\text{R}^{2}\)) (Allen, 1997). This can be made by creating a restricted model and then comparing it with a full model. Hence, the hypothesis can be schematized as follows.

\[ \begin{cases} \text{H}_{0}: \text{R}^{2}_{\text{res}} >= \text{R}^{2}_{\text{full}} \\ \text{H}_{a}: \text{R}^{2}_{\text{res}} < \text{R}^{2}_{\text{full}} \end{cases} \]

The general equation for the F-test (Allen, 1997, p. 113) :

\[ \text{F} = \cfrac{\text{R}^{2}_{F} - \text{R}^{2}_{R} / (k_{F} - k_{R})}{(1 - \text{R}^{2}_{F}) / (\text{N} - k_{F} - 1)} \]

Where:

  • \(\text{R}^{2}_{F}\) = Coefficient of determination for the full model;
  • \(\text{R}^{2}_{R}\) = Coefficient of determination for the restricted model;
  • \(k_{F}\) = Number of independent variables in the full model;
  • \(k_{R}\) = Number of independent variables in the restricted model;
  • \(\text{N}\) = Number of observations in the sample.

\[ \text{F} = \cfrac{\text{Additional Var. Explained} / \text{Additional d.f. Expended}}{\text{Var. unexplained} / \text{d.f. Remaining}} \]

It’s important to note that, in addition to the F-test, it’s assumed that for \(\text{R}^{2}_{\text{res}}\) to differ significantly from \(\text{R}^{2}_{\text{full}}\), there must be a non-negligible effect size between them. This effect size can be calculated using Cohen’s \(f^{2}\) (Cohen, 1988, 1992):

\[ f^{2} = \cfrac{\text{R}^{2}_{F} - \text{R}^{2}_{R}}{1 - \text{R}^{2}_{F}} \]

\[ f^{2} = \cfrac{\text{Additional Var. Explained}}{\text{Var. unexplained}} \]

E.2 A brief look on general linear models

See DeGroot & Schervish (2012, pp. 699–707, pp. 736-754) and Hair (2019, pp. 259–370) to learn more.

“[…] A problem of this type is called a problem of multiple linear regression because we are considering the regression of \(Y\) on \(k\) variables \(X_{1}, \dots, X_{k}\), rather than on just a single variable \(X\), and we are assuming also that this regression is a linear function of the parameters \(\beta_{0}, \dots, \beta_{k}\). In a problem of multiple linear regressions, we obtain \(n\) vectors of observations (\(x_{i1}. \dots, x_{ik}, Y_{i}\)), for \(i = 1, \dots, n\). Here \(x_{ij}\) is the observed value of the variable \(X_{j}\) for the \(i\)th observation. The \(E(Y)\) is given by the relation

\[ E(Y_{i}) = \beta_{0} + \beta_{1} x_{i1} + \dots + \beta_{k} x_{ik} \]

(DeGroot & Schervish, 2012, p. 738)

E.2.1 Definitions

Residuals/Fitted Values
For \(i = 1, \dots, n\), the observed values of \(\hat{y} = \hat{\beta}_{0} + \hat{\beta}_{1} x_{i}\) are called fitted values. For \(i = 1, \dots, n\), the observed values of \(e_{i} = y_{i} - \hat{y}_{i}\) are called residuals (DeGroot & Schervish, 2012, p. 717).

“[…] regression problems in which the observations \(Y_{i}, \dots, Y_{n}\) […] we shall assume that each observation \(Y_{i}\) has a normal distribution, that the observations \(Y_{1}, \dots, Y_{n}\) are independent, and that the observations \(Y_{1}, \dots, Y_{n}\) have the same variance \(\sigma^{2}\). Instead of a single predictor being associated with each \(Y_{i}\), we assume that a \(p\)-dimensional vector \(z_{i} = (z_{i0}, \dots, z_{ip - 1})\) is associated with each \(Y_{i}\)” (DeGroot & Schervish, 2012, p. 736).

General Linear Model
The statistical model in which the observations \(Y_{1}, \dots, Y_{n}\) satisfy the following assumptions (DeGroot & Schervish, 2012, p. 738).

E.2.2 Assumptions

Assumption 1
Predictor is known. Either the vectors \(z_{1}, \dots , z_{n}\) are known ahead of time, or they are the observed values of random vectors \(Z_{1}, \dots , Z_{n}\) on whose values we condition before computing the joint distribution of (\(Y_{1}, \dots , Y_{n}\)) (DeGroot & Schervish, 2012, p. 736).

Age and sex are known predictors for the chronotype (Roenneberg et al., 2007).

Assumption 2
Normality. For \(i = 1, \dots, n\), the conditional distribution of \(Y_{i}\) given the vectors \(z_{1}, \dots , z_{n}\) is a normal distribution (DeGroot & Schervish, 2012, p. 737).

(Normality of the error term distribution (Hair, 2019, p. 287)).

As it will be seen in the next topics, without any transformation, the chronotype variable does not have a normal distribution. However, this can be satisfied with a Box-Cox transformation (see Box & Cox (1964)).

A residual diagnostics will test the assumption of normality of the error term distribution.

Assumption 3
Linear mean. There is a vector of parameters \(\beta = (\beta_{0}, \dots, \beta_{p - 1})\) such that the conditional mean of \(Y_{i}\) given the values \(z_{1}, \dots , z_{n}\) has the form

\[ z_{i0} \beta_{0} + z_{i1} \beta_{1} + \cdots + z_{ip - 1} \beta_{p - 1} \]

for \(i = 1, \dots, n\) (DeGroot & Schervish, 2012, p. 737).

(Linearity of the phenomenon measured (Hair, 2019, p. 287)).

The hypothesis assumes a linear relation.

Assumption 4
Common variance. There is as parameter \(\sigma^{2}\) such the conditional variance of \(Y_{i}\) given the values \(z_{1}, \dots , z_{n}\) is \(\sigma^{2}\) for \(i = 1, \dots\, n\).

(Constant variance of the error terms (Hair, 2019, p. 287))

The presence of unequal variances (heteroscedasticity) will be tested with a residual diagnostics.

Assumption 5
Independence. The random variables \(Y_{1}, \dots , Y_{n}\) are independent given the observed \(z_{1}, \dots , z_{n}\) (DeGroot & Schervish, 2012, p. 737).

(Independence of the error terms (Hair, 2019, p. 287)).

This will also be tested with a residual diagnostics.

E.3 Data preparation

Outlier treatment (for now): 1.5x Interquartile range (IQR) for age and chronotype (MSFsc).

is_outlier <- function(x, method = "iqr", iqr_mult = 1.5, sd_mult = 3) {
  checkmate::assert_numeric(x)
  checkmate::assert_choice(method, c("iqr", "sd"))
  checkmate::assert_number(iqr_mult)
  checkmate::assert_number(sd_mult)

  if (method == "iqr") {
    iqr <- stats::IQR(x, na.rm = TRUE)
    min <- stats::quantile(x, 0.25, na.rm = TRUE) - (iqr_mult * iqr)
    max <- stats::quantile(x, 0.75, na.rm = TRUE) + (iqr_mult * iqr)
  } else if (method == "sd") {
    min <- mean(x, na.rm = TRUE) - (sd_mult * stats::sd(x, na.rm = TRUE))
    max <- mean(x, na.rm = TRUE) + (sd_mult * stats::sd(x, na.rm = TRUE))
  }

  dplyr::if_else(x >= min & x <= max, FALSE, TRUE, missing = FALSE)
}
source(here::here("R/utils.R"))

utc_minus_3_states <- c(
  "Amapá", "Pará", "Maranhão", "Tocantins", "Piauí", "Ceará",
  "Rio Grande do Norte", "Paraíba", "Pernambuco", "Alagoas", "Sergipe",
  "Bahia", "Distrito Federal", "Goiás", "Minas Gerais", "Espírito Santo",
  "Rio de Janeiro", "São Paulo", "Paraná", "Santa Catarina",
  "Rio Grande do Sul"
)

data <- 
  targets::tar_read("geocoded_data", store = here::here("_targets")) |>
  dplyr::filter(state %in% utc_minus_3_states) |>
  dplyr::select(msf_sc, age, sex, state, latitude, longitude) |>
  dplyr::mutate(msf_sc = transform_time(msf_sc)) |>
  tidyr::drop_na(msf_sc, age, sex, latitude)

E.4 Restricted model

E.4.1 Model building

box_cox <- MASS::boxcox(msf_sc ~ age + sex, data = data)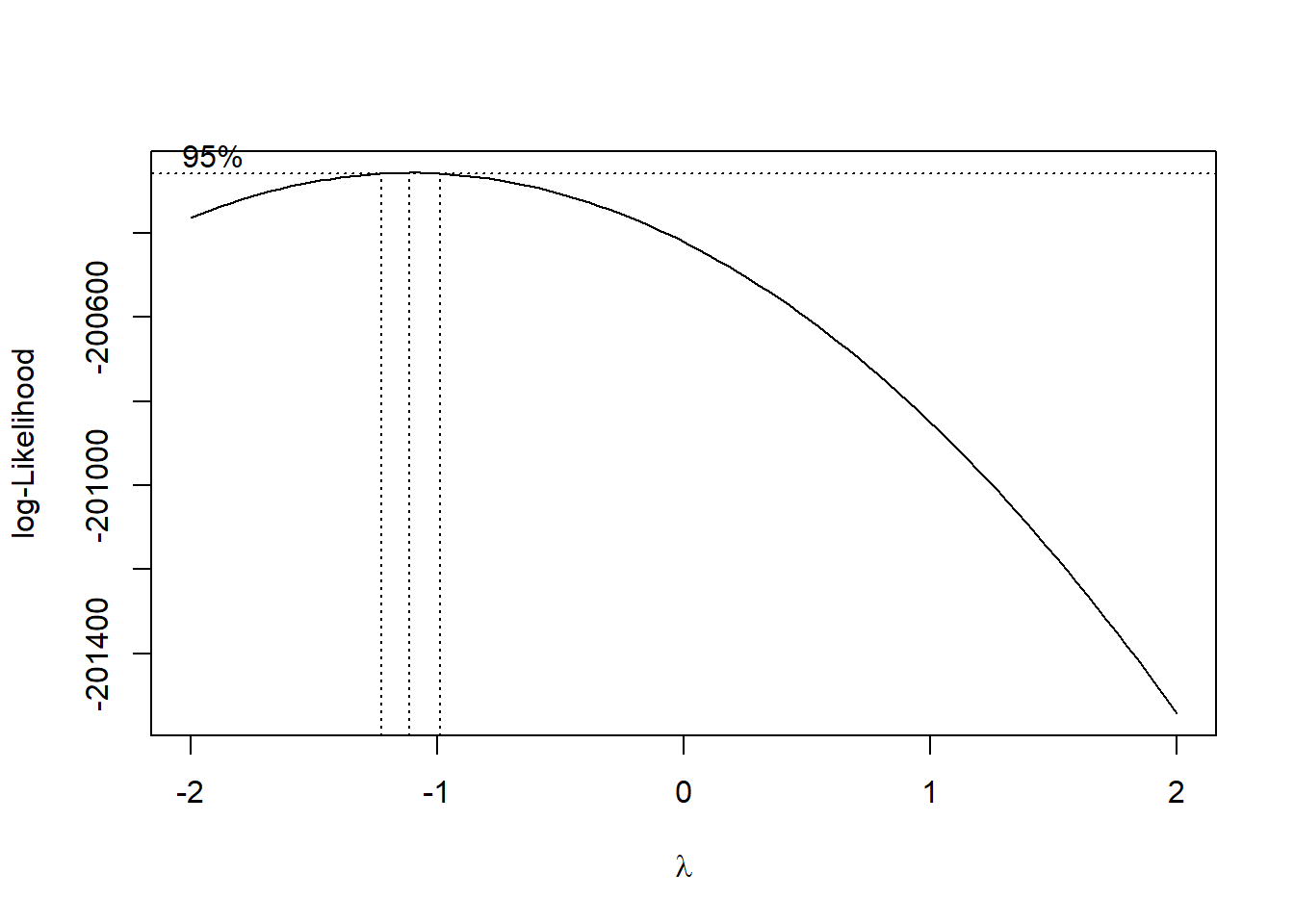

Source: Created by the author. See Box & Cox (1964) to learn more.

Table E.1: Profile of log-likelihoods for the parameter (\(\lambda\)) of the Box-Cox power transformation for the restricted model 
lambda <- box_cox$x[which.max(box_cox$y)]

lambda
#> [1] -1.1111
res_model <- stats::lm(
  ((msf_sc^lambda - 1) / lambda) ~ age + sex, data = data
)
broom::tidy(res_model)
term estimate std.error statistic p.value
(Intercept) 0.9 0 513579298.250 0
age 0.0 0 -65.128 0
sexMale 0.0 0 13.020 0

Source: Created by the author.

Table E.2: Summarized information about the components of the restricted model 
broom::glance(res_model) |> tidyr::pivot_longer(cols = dplyr::everything())
name value
r.squared 0.05373
adj.r.squared 0.05371
sigma 0.00000
statistic 2178.87560
p.value 0.00000
df 2.00000
logLik 1106194.89709
AIC -2212381.79419
BIC -2212344.80126
deviance 0.00000
df.residual 76741.00000
nobs 76744.00000

Source: Created by the author.

Table E.3: Summarized statistics about the restricted model 
res_model |> summary()
#> 
#> Call:
#> stats::lm(formula = ((msf_sc^lambda - 1)/lambda) ~ age + sex, 
#>     data = data)
#> 
#> Residuals:
#>           Min            1Q        Median            3Q           Max 
#> -0.0000004859 -0.0000000911 -0.0000000031  0.0000000916  0.0000004204 
#> 
#> Coefficients:
#>                     Estimate       Std. Error     t value Pr(>|t|)    
#> (Intercept)  0.8999976603602  0.0000000017524 513579298.2   <2e-16 ***
#> age         -0.0000000033812  0.0000000000519       -65.1   <2e-16 ***
#> sexMale      0.0000000132309  0.0000000010162        13.0   <2e-16 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Residual standard error: 0.000000133 on 76741 degrees of freedom
#> Multiple R-squared:  0.0537, Adjusted R-squared:  0.0537 
#> F-statistic: 2.18e+03 on 2 and 76741 DF,  p-value: <2e-16

E.4.2 Residual diagnostics

E.4.2.1 Normality

source(here::here("R/stats_sum.R"))
source(here::here("R/utils.R"))

res_model |>
  stats::residuals() |>
  stats_sum(print = FALSE) |>
  list_as_tibble()
name value
n 76744
n_rm_na 76744
n_na 0
mean 6.60699976667332e-23
var 0.0000000000000176852866826985
sd 0.000000132986039427823
min -0.000000485865195534305
q_1 -0.0000000911138016567908
median -0.00000000313530324787135
q_3 0.000000091553820345483
max 0.000000420368932360539
iqr 0.000000182667622002274
skewness -0.0105262146639209
kurtosis 2.82813923301771

Source: Created by the author.

Table E.4: Statistics about the restricted model residuals.

It is important to note that the Kolmogorov-Smirnov and Pearson chi-square test are here just for reference since many authors don’t recommend using them when testing for normality (D’Agostino & Belanger, 1990).

Learn more about normality tests in Thode (2002).

\[ \begin{cases} \text{H}_{0}: \text{Normality} \\ \text{H}_{a}: \text{Nonnormality} \end{cases} \]

source(here::here("R/normality_sum.R"))

res_model |>
  stats::residuals() |>
  normality_sum()
test p_value
Anderson-Darling 0.00000
Bonett-Seier 0.00000
Cramer-von Mises 0.00000
D’Agostino Omnibus Test NA
D’Agostino Skewness Test 0.23383
D’Agostino Kurtosis Test NA
Jarque–Bera 0.00000
Lilliefors (K-S) 0.00000
Pearson chi-square 0.00000
Shapiro-Francia NA
Shapiro-Wilk NA

Source: Created by the author.

Table E.5: Normality tests about the restricted model residuals

Correlation between observed residuals and expected residuals under normality.

res_model |> olsrr::ols_test_correlation()
#> [1] 0.99929
source(here::here("R/test_normality.R"))

# res_model |> olsrr::ols_plot_resid_qq()

qq_plot <- res_model |> 
  stats::residuals() |>
  plot_qq(print = FALSE)

hist_plot <- res_model |>
  stats::residuals() |>
  plot_hist(print = FALSE)

cowplot::plot_grid(hist_plot, qq_plot, ncol = 2, nrow = 1)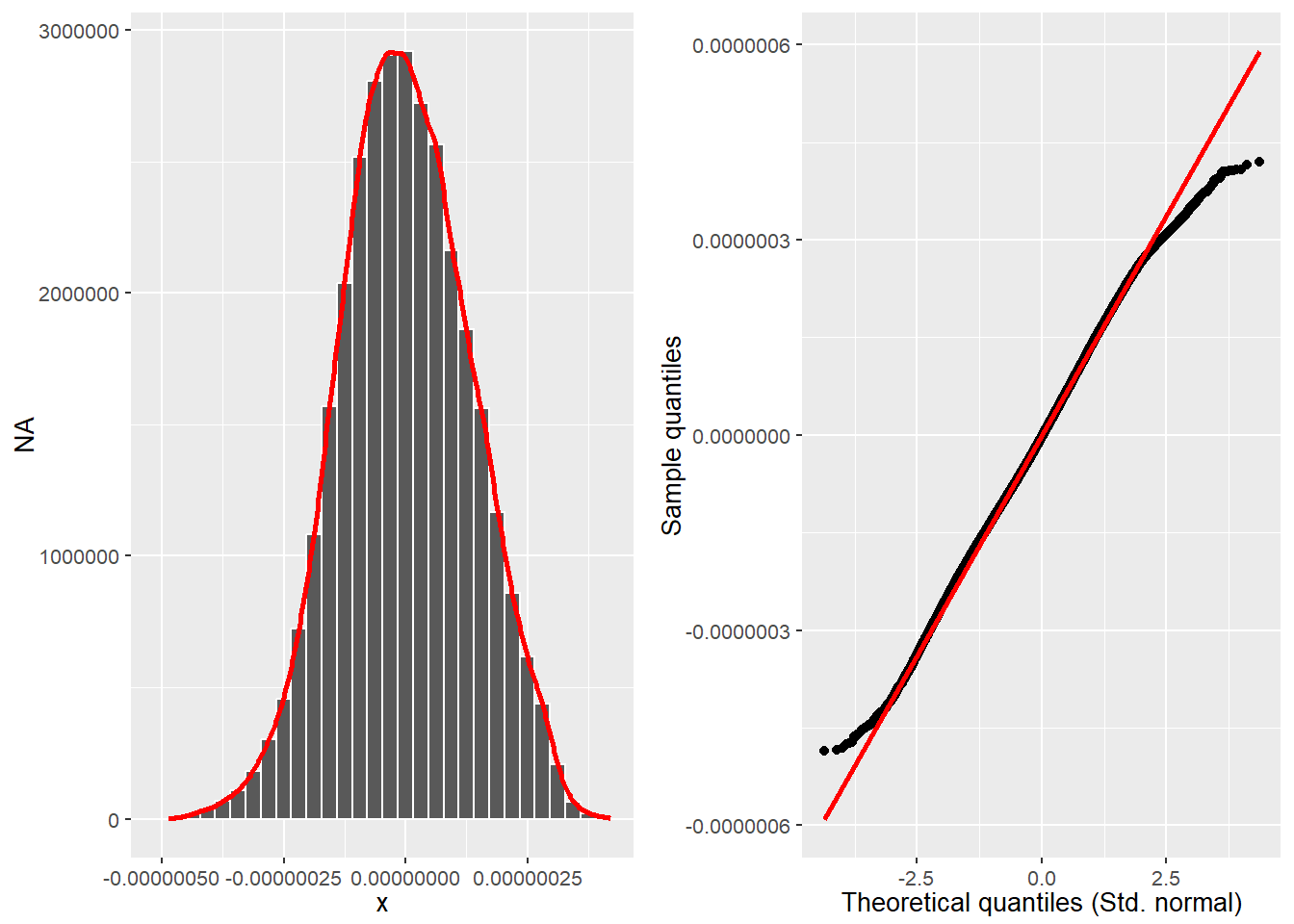

Source: Created by the author.

Figure E.1: Histogram of the restricted model residuals with a kernel density estimate, along with a quantile-quantile (Q-Q) plot between the residuals and the theoretical quantiles of the normal distribution

E.4.2.2 Common variance

res_model |> olsrr::ols_plot_resid_fit()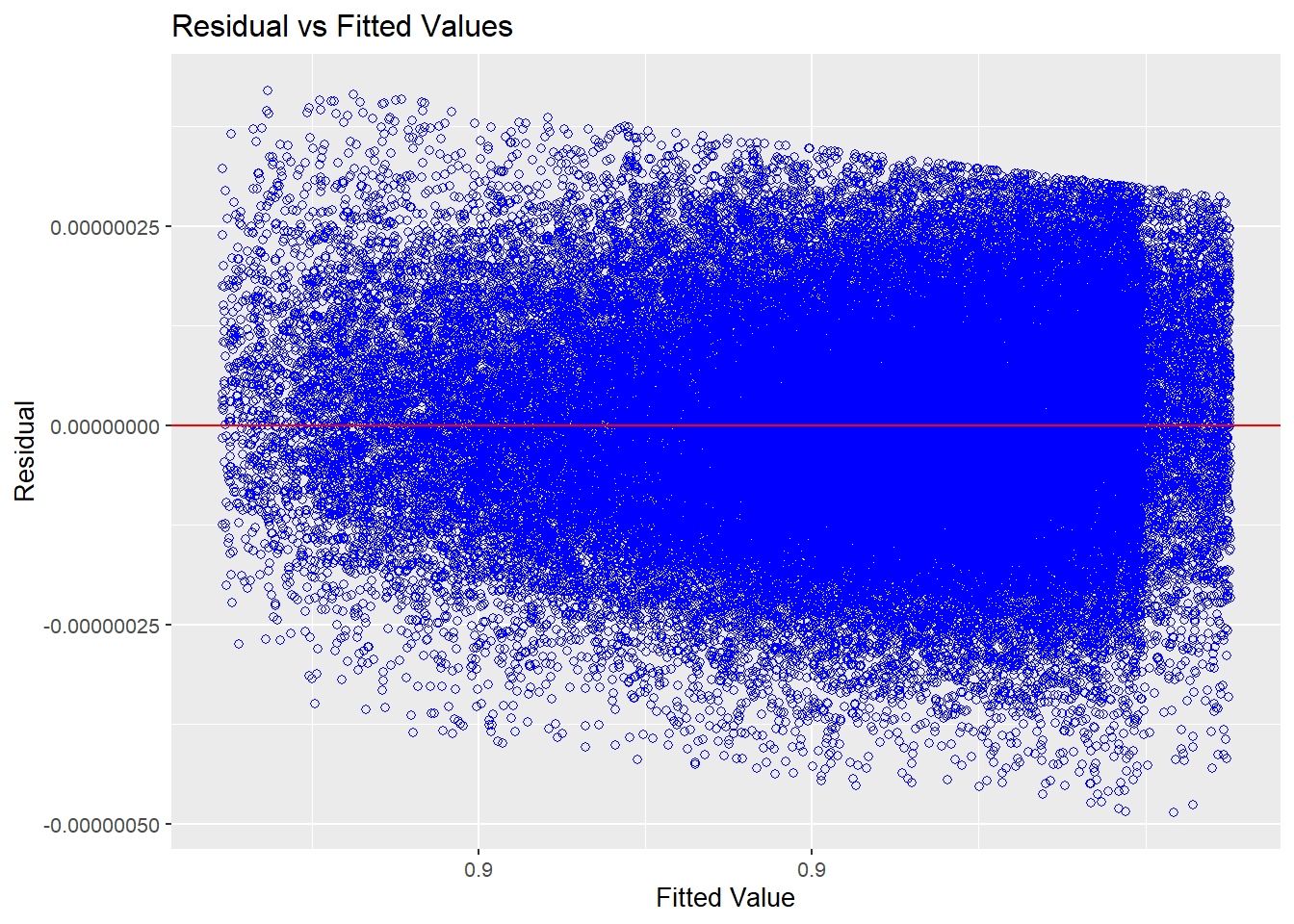

Source: Created by the author.

Figure E.2: Relation between the fitted values of the restricted model and its residuals. 
res_model |> plot(3)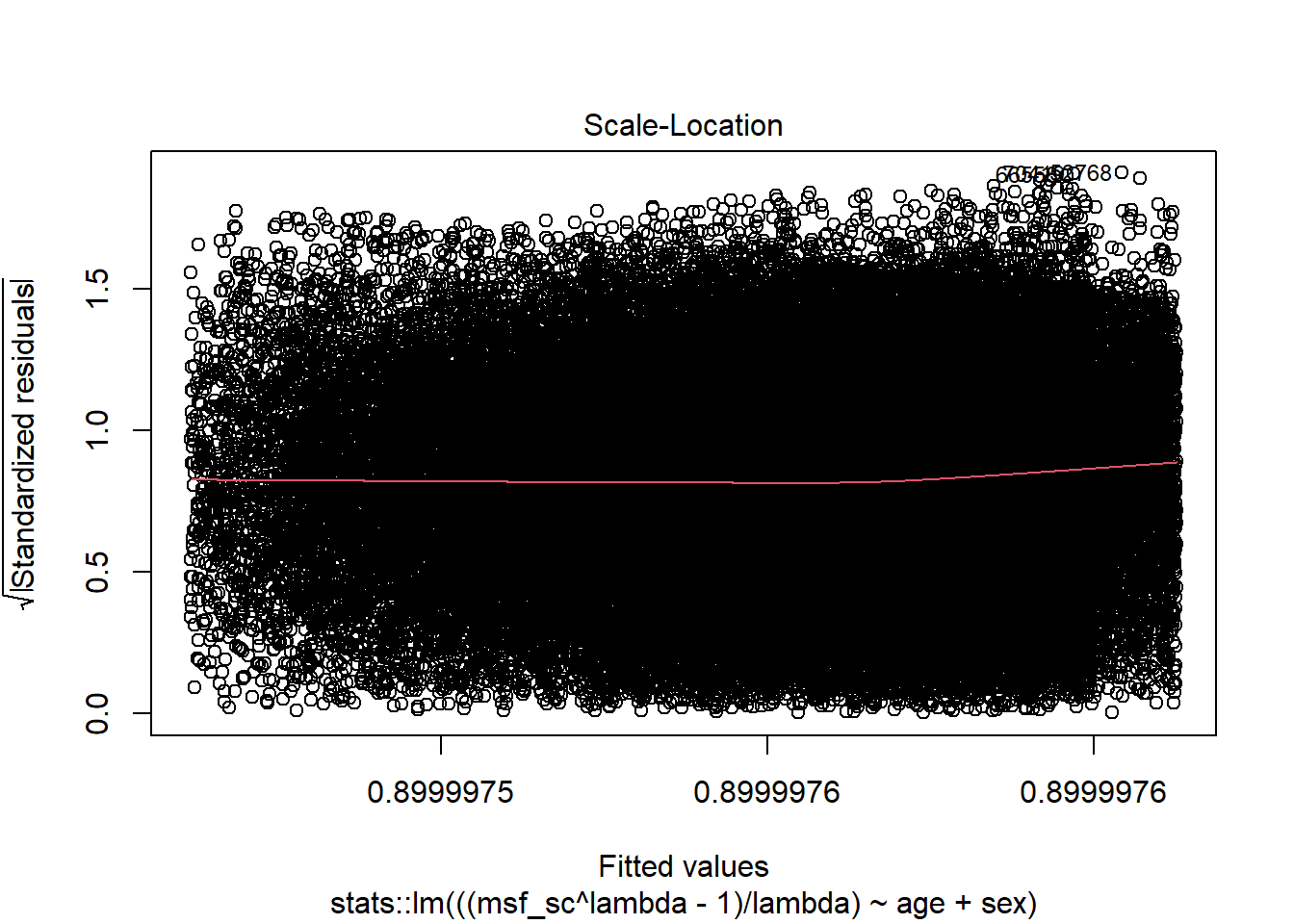

Source: Created by the author.

Figure E.3: Relation between the fitted values of the restricted model and its standardized residuals 
res_model |> olsrr::ols_test_breusch_pagan()
#> 
#>  Breusch Pagan Test for Heteroskedasticity
#>  -----------------------------------------
#>  Ho: the variance is constant            
#>  Ha: the variance is not constant        
#> 
#>                           Data                           
#>  --------------------------------------------------------
#>  Response : ((msf_sc^lambda - 1)/lambda) 
#>  Variables: fitted values of ((msf_sc^lambda - 1)/lambda) 
#> 
#>         Test Summary          
#>  -----------------------------
#>  DF            =    1 
#>  Chi2          =    70149.3586 
#>  Prob > Chi2   =    0.0000
res_model |> olsrr::ols_test_score()
#> 
#>  Score Test for Heteroskedasticity
#>  ---------------------------------
#>  Ho: Variance is homogenous
#>  Ha: Variance is not homogenous
#> 
#>  Variables: fitted values of ((msf_sc^lambda - 1)/lambda) 
#> 
#>       Test Summary       
#>  ------------------------
#>  DF            =    1 
#>  Chi2          =    0.000 
#>  Prob > Chi2   =    1.000

E.4.2.3 Independence

Variance inflation factor (VIF)
“Indicator of the effect that the other independent variables have on the standard error of a regression coefficient. The variance inflation factor is directly related to the tolerance value (\(\text{VIF}_{i} = 1/\text{TO}L\)). Large VIF values also indicate a high degree of collinearity or multicollinearity among the independent variables” (Hair, 2019, p. 265). 
res_model |> olsrr::ols_coll_diag()
#> Tolerance and Variance Inflation Factor
#> ---------------------------------------
#>   Variables Tolerance    VIF
#> 1       age    0.9988 1.0012
#> 2   sexMale    0.9988 1.0012
#> 
#> 
#> Eigenvalue and Condition Index
#> ------------------------------
#>   Eigenvalue Condition Index intercept      age   sexMale
#> 1   2.422418          1.0000  0.011753 0.011936 0.0669897
#> 2   0.538450          2.1211  0.015824 0.018848 0.9280439
#> 3   0.039132          7.8679  0.972423 0.969216 0.0049664

E.4.2.4 Measures of influence

Leverage points
“Type of influential observation defined by one aspect of influence termed leverage. These observations are substantially different on one or more independent variables, so that they affect the estimation of one or more regression coefficients” (Hair, 2019, p. 262). 
res_model |> olsrr::ols_plot_resid_lev()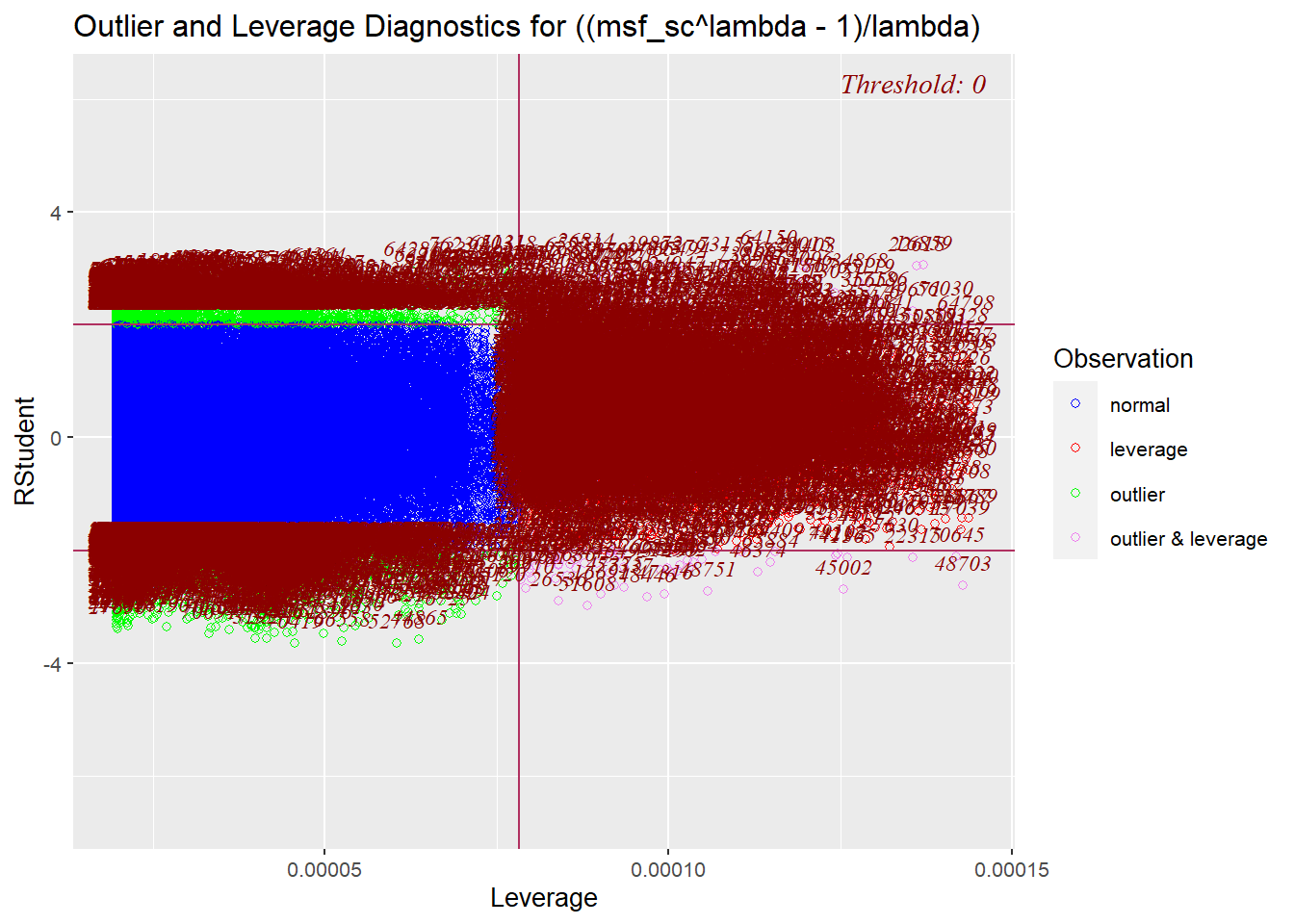

Source: Created by the author.

Figure E.4: Relation between the restricted model studentized residuals and their leverage/influence

E.5 Full model

E.5.1 Model building

box_cox <- MASS::boxcox(
  msf_sc ~ age + sex + latitude, data = data
  )

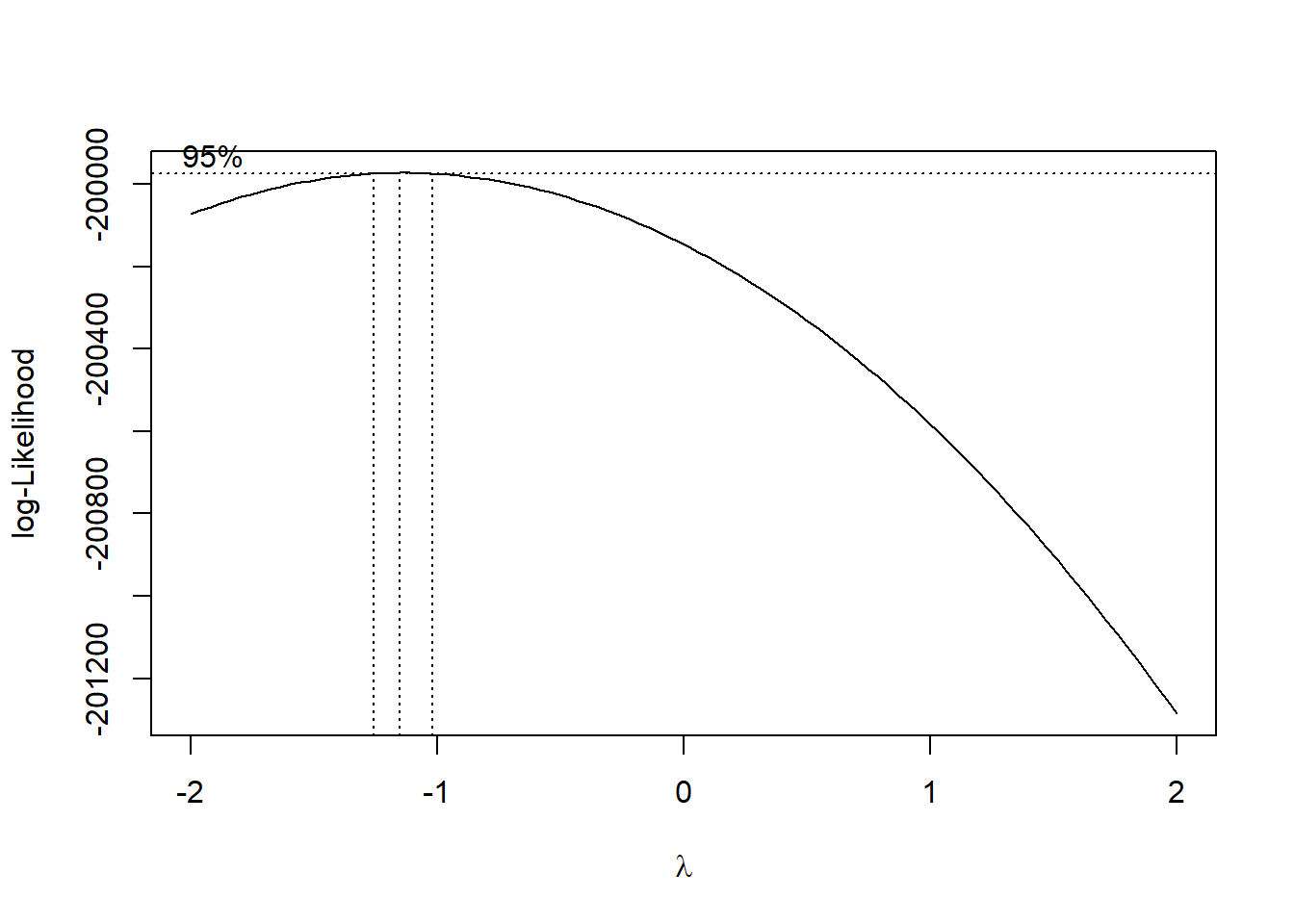
Source: Created by the author. See Box & Cox (1964) to learn more.

Table E.6: Profile of log-likelihoods for the parameter (\(\lambda\)) of the Box-Cox power transformation for the full model 
box_cox$x[which.max(box_cox$y)] # lambda
#> [1] -1.1515
lambda # The same lambda of the restricted model
#> [1] -1.1111
full_model <- stats::lm(
  ((msf_sc^lambda - 1) / lambda) ~ age + sex + latitude, 
  data = data
  )
broom::tidy(full_model)
term estimate std.error statistic p.value
(Intercept) 0.9 0 391908052.847 0
age 0.0 0 -66.928 0
sexMale 0.0 0 13.558 0
latitude 0.0 0 -23.852 0

Source: Created by the author.

Table E.7: Summarized information about the components of the full model 
broom::glance(full_model) |>
  tidyr::pivot_longer(cols = dplyr::everything())
name value
r.squared 0.06070
adj.r.squared 0.06066
sigma 0.00000
statistic 1652.97928
p.value 0.00000
df 3.00000
logLik 1106478.33068
AIC -2212946.66136
BIC -2212900.42021
deviance 0.00000
df.residual 76740.00000
nobs 76744.00000

Source: Created by the author.

Table E.8: Summarized statistics about the full model 
full_model |> summary()
#> 
#> Call:
#> stats::lm(formula = ((msf_sc^lambda - 1)/lambda) ~ age + sex + 
#>     latitude, data = data)
#> 
#> Residuals:
#>           Min            1Q        Median            3Q           Max 
#> -0.0000004874 -0.0000000911 -0.0000000034  0.0000000912  0.0000004328 
#> 
#> Coefficients:
#>                     Estimate       Std. Error     t value Pr(>|t|)    
#> (Intercept)  0.8999976247783  0.0000000022965 391908052.9   <2e-16 ***
#> age         -0.0000000034710  0.0000000000519       -66.9   <2e-16 ***
#> sexMale      0.0000000137296  0.0000000010127        13.6   <2e-16 ***
#> latitude    -0.0000000018222  0.0000000000764       -23.9   <2e-16 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> 
#> Residual standard error: 0.000000132 on 76740 degrees of freedom
#> Multiple R-squared:  0.0607, Adjusted R-squared:  0.0607 
#> F-statistic: 1.65e+03 on 3 and 76740 DF,  p-value: <2e-16

E.5.2 Residual diagnostics

E.5.2.1 Normality

source(here::here("R/stats_sum.R"))
source(here::here("R/utils.R"))

full_model |>
  stats::residuals() |>
  stats_sum(print = FALSE) |> 
  list_as_tibble()
name value
n 76744
n_rm_na 76744
n_na 0
mean 4.85272564733669e-24
var 0.0000000000000175551361304561
sd 0.00000013249579665203
min -0.000000487410752460545
q_1 -0.0000000910649425186321
median -0.000000003374344652286
q_3 0.0000000911899588839585
max 0.000000432826012898983
iqr 0.000000182254901402591
skewness 0.000655994107765645
kurtosis 2.82688323293117

Source: Created by the author.

Table E.9: Statistics about the full model residuals

It is important to note that the Kolmogorov-Smirnov and Pearson chi-square test are here just for reference since some authors don’t recommend using them when testing for normality (D’Agostino & Belanger, 1990).

\[ \begin{cases} \text{H}_{0}: \text{Normality} \\ \text{H}_{a}: \text{Nonnormality} \end{cases} \]

source(here::here("R/normality_sum.R"))

full_model |>
  stats::residuals() |>
  normality_sum()
test p_value
Anderson-Darling 0.00000
Bonett-Seier 0.00000
Cramer-von Mises 0.00000
D’Agostino Omnibus Test NA
D’Agostino Skewness Test 0.94085
D’Agostino Kurtosis Test NA
Jarque–Bera 0.00000
Lilliefors (K-S) 0.00000
Pearson chi-square 0.00000
Shapiro-Francia NA
Shapiro-Wilk NA

Source: Created by the author.

Table E.10: Normality tests about the full model residuals.

Correlation between observed residuals and expected residuals under normality

full_model |> olsrr::ols_test_correlation()
#> [1] 0.99929
source(here::here("R/test_normality.R"))

hist_plot <- full_model |>
  stats::residuals() |>
  plot_hist(print = FALSE)

qq_plot <- full_model |> 
  stats::residuals() |>
  plot_qq(print = FALSE)

cowplot::plot_grid(hist_plot, qq_plot, ncol = 2, nrow = 1)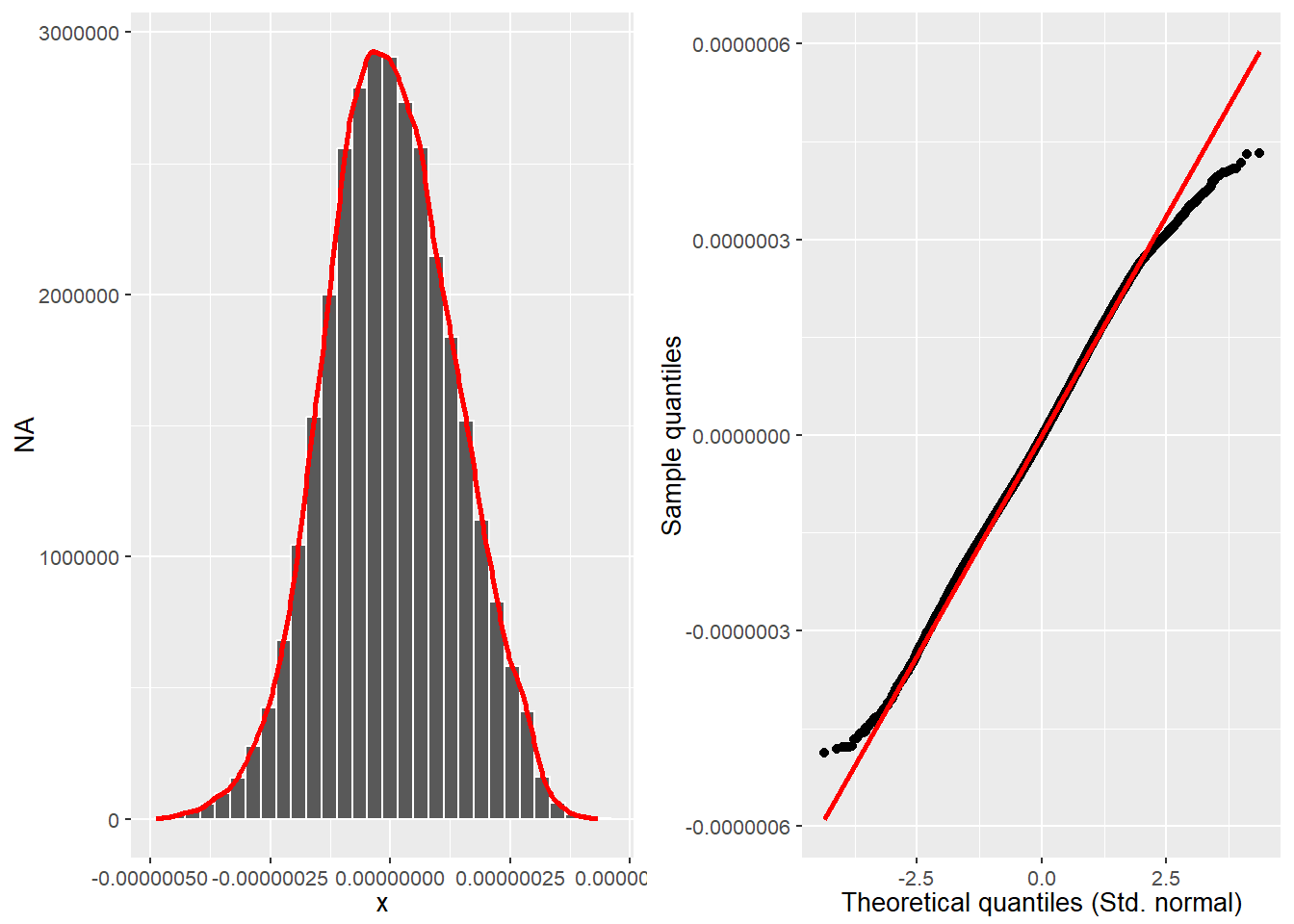

Source: Created by the author.

Figure E.5: Histogram of the full model residuals with a kernel density estimate, along with a quantile-quantile (Q-Q) plot between the residuals and the theoretical quantiles of the normal distribution

E.5.2.2 Common variance

full_model |> olsrr::ols_plot_resid_fit()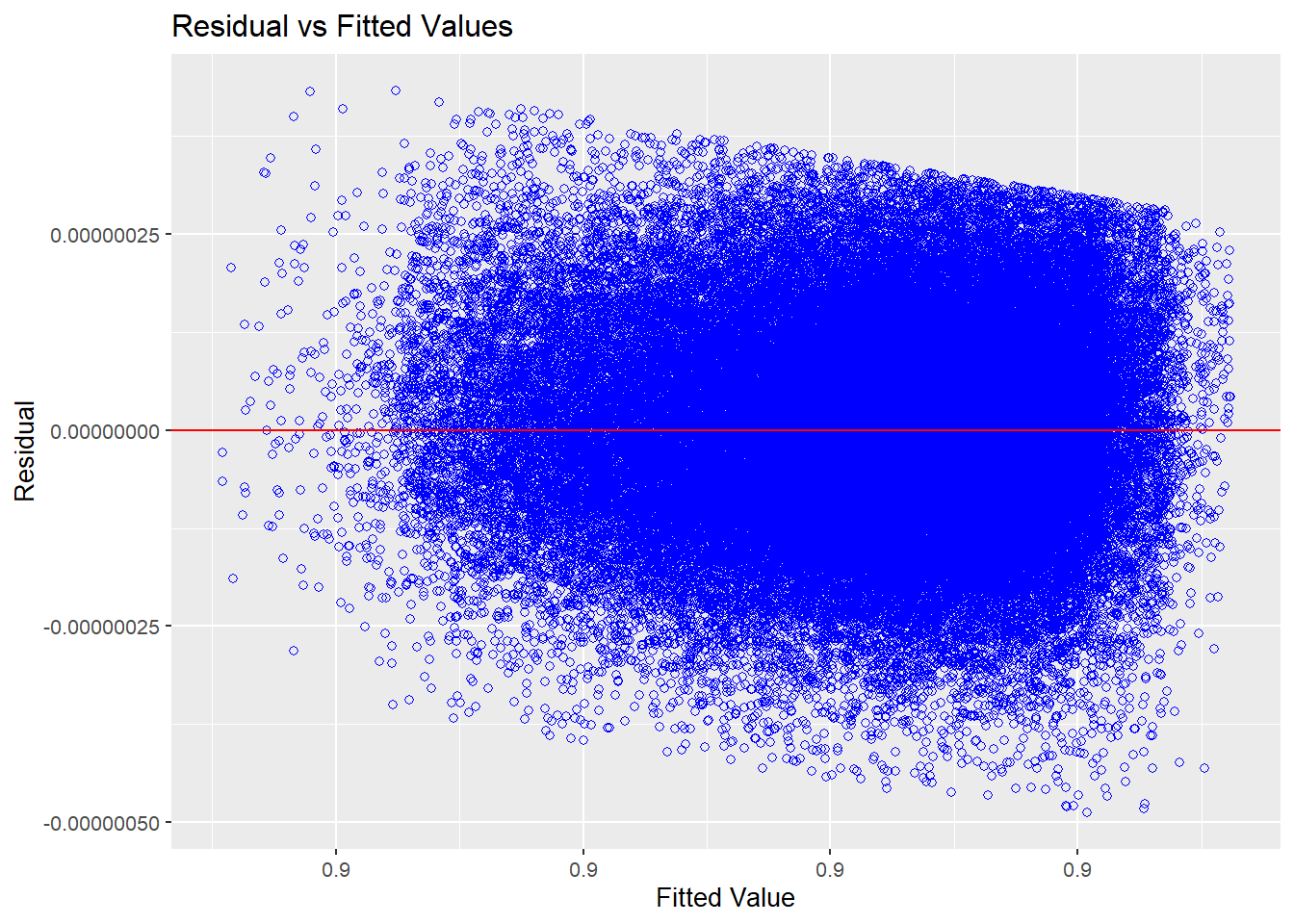

Source: Created by the author.

Figure E.6: Relation between the fitted values of the full model and its residuals 
full_model |> plot(3)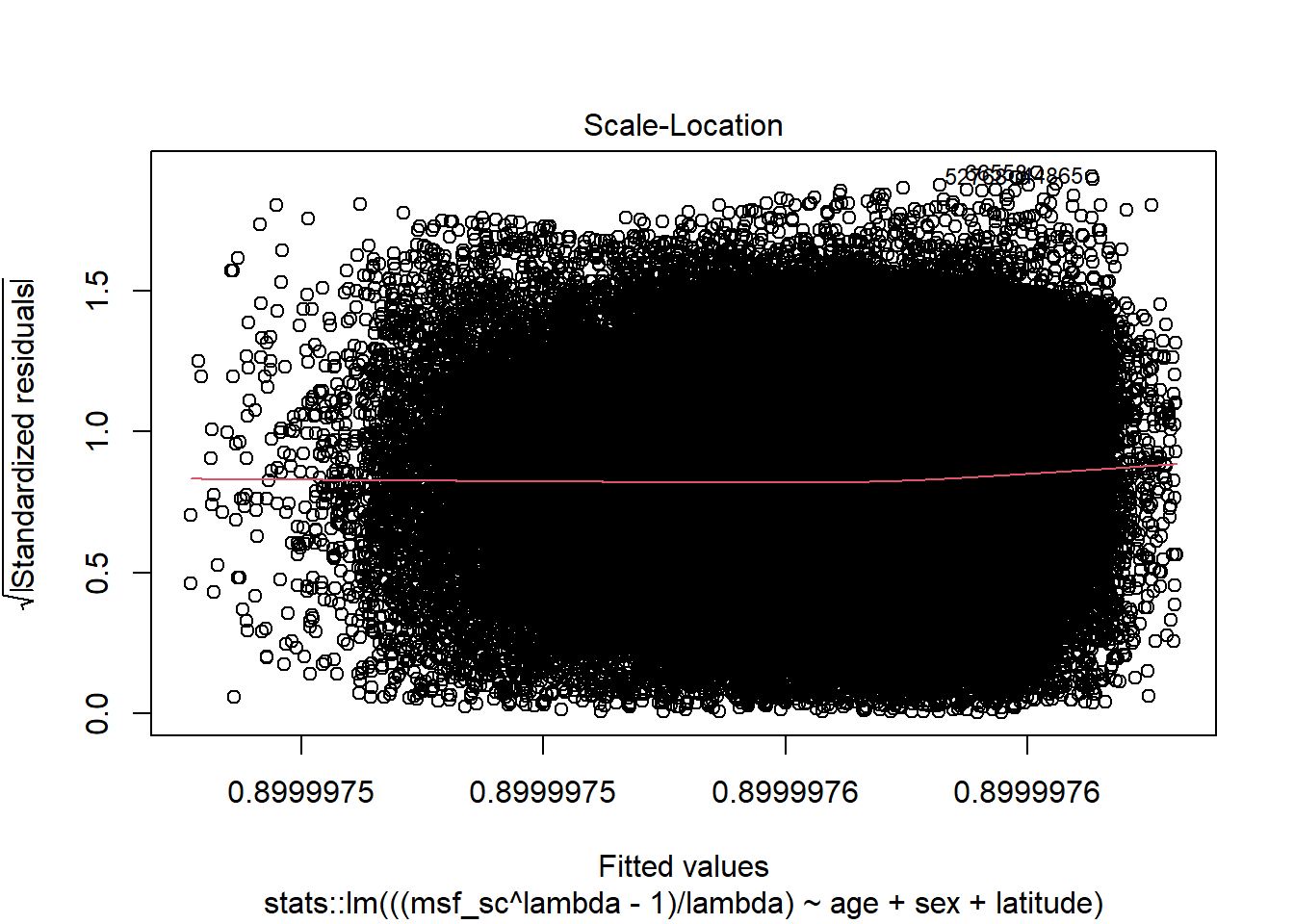

Source: Created by the author.

Figure E.7: Relation between the fitted values of the full model and its standardized residuals 
full_model |> olsrr::ols_test_breusch_pagan()
#> 
#>  Breusch Pagan Test for Heteroskedasticity
#>  -----------------------------------------
#>  Ho: the variance is constant            
#>  Ha: the variance is not constant        
#> 
#>                           Data                           
#>  --------------------------------------------------------
#>  Response : ((msf_sc^lambda - 1)/lambda) 
#>  Variables: fitted values of ((msf_sc^lambda - 1)/lambda) 
#> 
#>         Test Summary          
#>  -----------------------------
#>  DF            =    1 
#>  Chi2          =    70101.1634 
#>  Prob > Chi2   =    0.0000
full_model |> olsrr::ols_test_score()
#> 
#>  Score Test for Heteroskedasticity
#>  ---------------------------------
#>  Ho: Variance is homogenous
#>  Ha: Variance is not homogenous
#> 
#>  Variables: fitted values of ((msf_sc^lambda - 1)/lambda) 
#> 
#>       Test Summary       
#>  ------------------------
#>  DF            =    1 
#>  Chi2          =    0.000 
#>  Prob > Chi2   =    1.000

E.5.2.3 Independence

Variance inflation factor (VIF)
“Indicator of the effect that the other independent variables have on the standard error of a regression coefficient. The variance inflation factor is directly related to the tolerance value (\(\text{VIF}_{i} = 1/\text{TO}L\)). Large VIF values also indicate a high degree of collinearity or multicollinearity among the independent variables” (Hair, 2019, p. 265). 
full_model |> olsrr::ols_coll_diag()
#> Tolerance and Variance Inflation Factor
#> ---------------------------------------
#>   Variables Tolerance    VIF
#> 1       age   0.99354 1.0065
#> 2   sexMale   0.99838 1.0016
#> 3  latitude   0.99441 1.0056
#> 
#> 
#> Eigenvalue and Condition Index
#> ------------------------------
#>   Eigenvalue Condition Index  intercept       age   sexMale  latitude
#> 1   3.312504          1.0000 0.00377395 0.0064918 0.0304493 0.0068553
#> 2   0.584652          2.3803 0.00328127 0.0064143 0.9588857 0.0083393
#> 3   0.073700          6.7042 0.00040414 0.5063551 0.0023826 0.5659326
#> 4   0.029145         10.6609 0.99254063 0.4807389 0.0082824 0.4188728

E.5.2.4 Measures of influence

Leverage points
“Type of influential observation defined by one aspect of influence termed leverage. These observations are substantially different on one or more independent variables, so that they affect the estimation of one or more regression coefficients” (Hair, 2019, p. 262). 
full_model |> olsrr::ols_plot_resid_lev()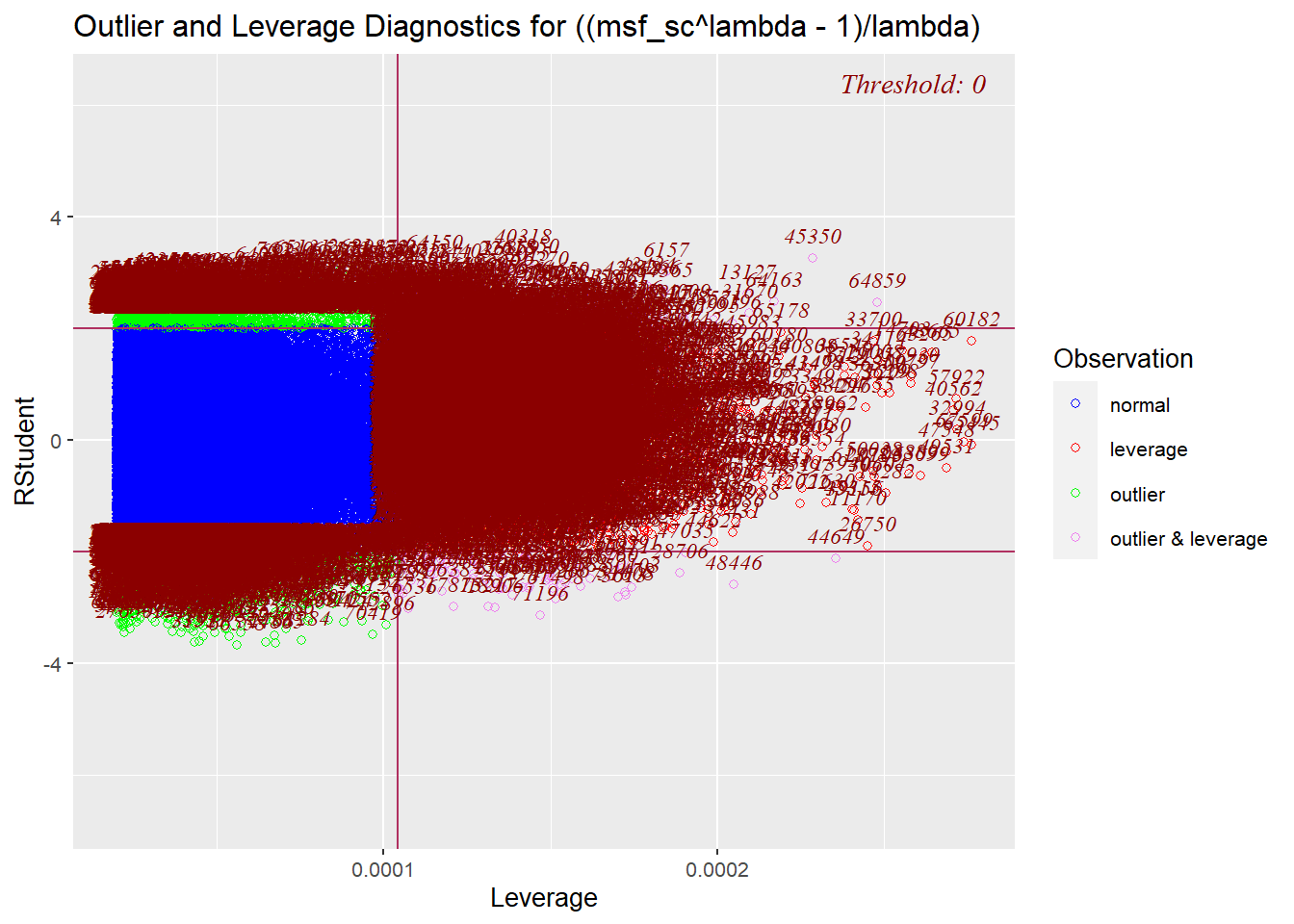

Source: Created by the author.

Figure E.8: Relation between the full model studentized residuals and their leverage/influence

E.6 Hypothesis test

\[ \begin{cases} \text{H}_{0}: \text{R}^{2}_{\text{res}} >= \text{R}^{2}_{\text{full}} \\ \text{H}_{a}: \text{R}^{2}_{\text{res}} < \text{R}^{2}_{\text{full}} \end{cases} \]

\[ \text{F} = \cfrac{\text{R}^{2}_{F} - \text{R}^{2}_{R} / (k_{F} - k_{R})}{(1 - \text{R}^{2}_{F}) / (\text{N} - k_{F} - 1)} \]

\[ \text{F} = \cfrac{\text{Additional Var. Explained} / \text{Additional d.f. Expended}}{\text{Var. unexplained} / \text{d.f. Remaining}} \]

source(here::here("R/utils-stats.R"))

dplyr::tibble(
  name = c("r_squared_res", "r_squared_full", "diff"),
  value = c(
  r_squared(res_model), r_squared(full_model), 
  r_squared(full_model) - r_squared(res_model)
  )
)
name value
r_squared_res 0.05373
r_squared_full 0.06070
diff 0.00696

Source: Created by the author.

Table E.11: Comparison between the coefficients of determination (\(\text{R}^2\)) of the restricted and full model 
print(stats::anova(res_model, full_model))
#> Analysis of Variance Table
#> 
#> Model 1: ((msf_sc^lambda - 1)/lambda) ~ age + sex
#> Model 2: ((msf_sc^lambda - 1)/lambda) ~ age + sex + latitude
#>   Res.Df           RSS Df        Sum of Sq   F Pr(>F)    
#> 1  76741 0.00000000136                                   
#> 2  76740 0.00000000135  1 0.00000000000999 569 <2e-16 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
source(here::here("R/utils-stats.R"))

n <- nrow(data)
k_res <- length(stats::coefficients(res_model)) - 1
k_full <- length(stats::coefficients(full_model)) - 1

((r_squared(full_model) - r_squared(res_model)) / (k_full - k_res)) / 
  ((1 - r_squared(full_model)) / (n  - k_full - 1))
#> [1] 568.94

\[ f^{2} = \cfrac{\text{R}^{2}_{F} - \text{R}^{2}_{R}}{1 - \text{R}^{2}_{F}} \]

\[ f^{2} = \cfrac{\text{Additional Var. Explained}}{\text{Var. unexplained}} \]

source(here::here("R/cohens_f_squared.R"))
source(here::here("R/utils-stats.R"))

cohens_f_squared_summary(
  adj_r_squared(res_model), 
  adj_r_squared(full_model)
  )
name value
f_squared 0.00740068896515648
effect_size Negligible

Source: Created by the author. See Cohen (1988) and Cohen (1992) to learn more.

Table E.12: Effect size between the restricted and full model based on Cohen’s \(f^2\)