1  [Showcase] Introduction

The text below is for demonstrative purposes only.

See https://github.com/danielvartan/abnt to learn more about this template.

See Figure 1.1.

“The activity can be represented by a general schema of problem-solving by the method of imaginative conjectures and criticism, or, as I have often called it, by the method of conjecture and refutation. The schema (in its simplest form) is this

\[ \text{P}_{1} \to \text{TT} \to \text{EE} \to \text{P}_{2} \]

Here \(\text{P}_{1}\) is the problem from which we start, \(\text{TT}\) (the ‘tentative theory’) is the imaginative conjectural solution which we first reach, for example our first tentative interpretation. \(\text{EE}\) (‘error- elimination’) consists of a severe critical examination of our conjecture, our tentative interpretation: it consists, for example, of the critical use of documentary evidence and, if we have at this early stage more than one conjecture at our disposal, it will also consist of a critical discussion and comparative evaluation of the competing conjectures. \(\text{P}_{2}\) is the problem situation as it emerges from our first critical attempt to solve our problems.

It leads up to our second attempt (and so on). A satisfactory understanding will be reached if the interpretation, the conjectural theory, finds support in the fact that it can throw new light on new problems — on more problems than we expected; or if it finds support in the fact that it explains many sub-problems, some of which were not seen to start with. Thus we may say that we can gauge the progress we have made by comparing \(\text{P}_{1}\) with some of our later problems (\(\text{P}_{n}\), say).”

(POPPER, 1979, p. 164)

Source: Steve Pyke.

Figure 1.1: Karl Popper (July 25, 1902 – September 17, 1994).
One of the 20th century’s most influential philosophers of science.

1.1 Secondary section

See Table 1.1.

Code
datasets::iris |>
  dplyr::as_tibble() |>
  dplyr::slice_sample(n = 5) |>
  gt::gt()
Sepal.Length Sepal.Width Petal.Length Petal.Width Species
6.5 3.0 5.5 1.8 virginica
6.5 3.0 5.8 2.2 virginica
5.0 3.0 1.6 0.2 setosa
5.0 3.5 1.6 0.6 setosa
6.2 2.9 4.3 1.3 versicolor

Source: Based on FISHER (1936).

Table 1.1: A sample of the famous (Fisher’s or Anderson’s) iris data set

1.1.1 Tertiary section

Code
ggplot2::ggplot(
  data = datasets::faithful, 
  mapping = ggplot2::aes(x = eruptions, y = waiting)
  ) +
  ggplot2::geom_point() +
  ggplot2::xlim(0.5, 6) +
  ggplot2::ylim(40, 110) +
  ggplot2::geom_density_2d_filled(alpha = 0.5) +
  ggplot2::geom_density_2d(linewidth = 0.25, colour = "black") +
  ggplot2::theme(legend.position = "none")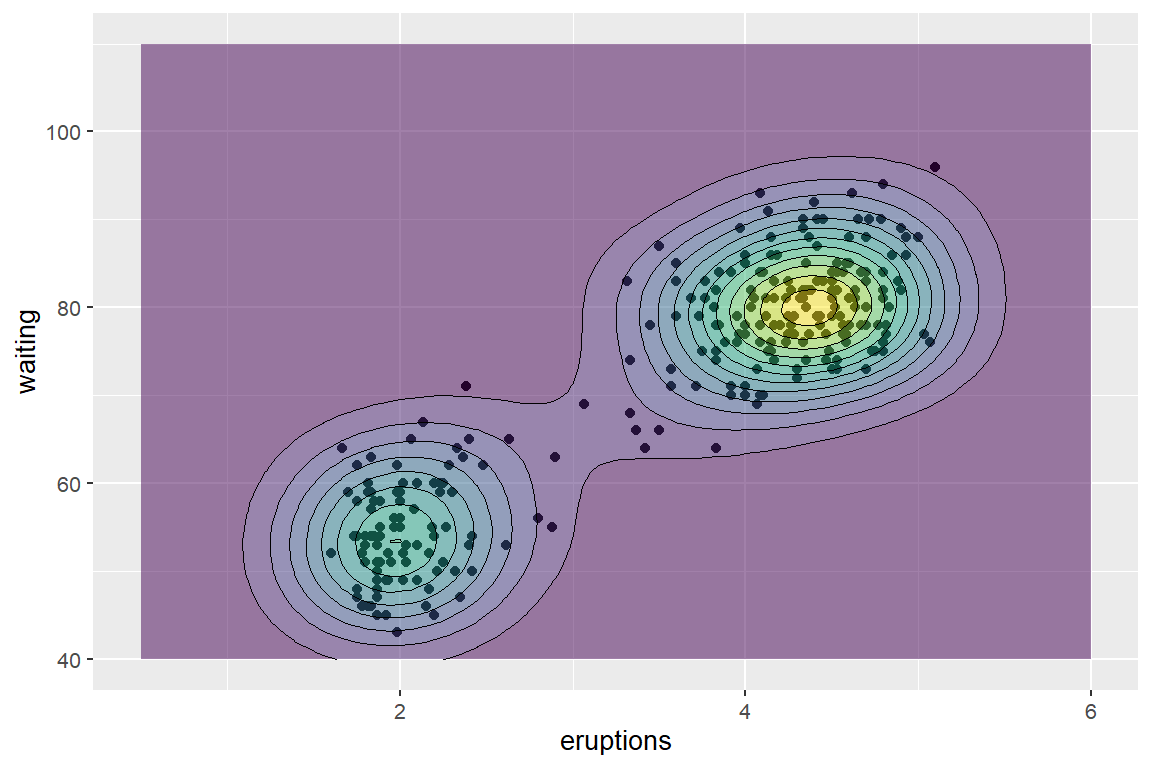

Source: Retrieved from the ggplot2 R package documentation (WICKHAM, 2016).

Figure 1.2: Relationship between waiting time to next eruption (minutes) and eruption time (minutes) at Old Faithful Geyser, Yellowstone National Park, Wyoming, USA

1.1.1.1 Quaternary section

  • Bullet point
    • Bullet point
      • Bullet point
1.1.1.1.1 Quinary section
  1. List
  2. List
  3. List

1.2 Another secondary section

See Figure 1.3.

Code
p <- ggplot2::ggplot(
  data = datasets::mtcars, 
  mapping = ggplot2::aes(x=wt, y=mpg, color=cyl, size=cyl)
  ) +
  ggplot2::geom_point() +
  ggplot2::theme(legend.position="none")

ggExtra::ggMarginal(
  p = p, 
  type = "histogram", 
  fill = "slateblue", 
  xparams = list(bins=10)
)

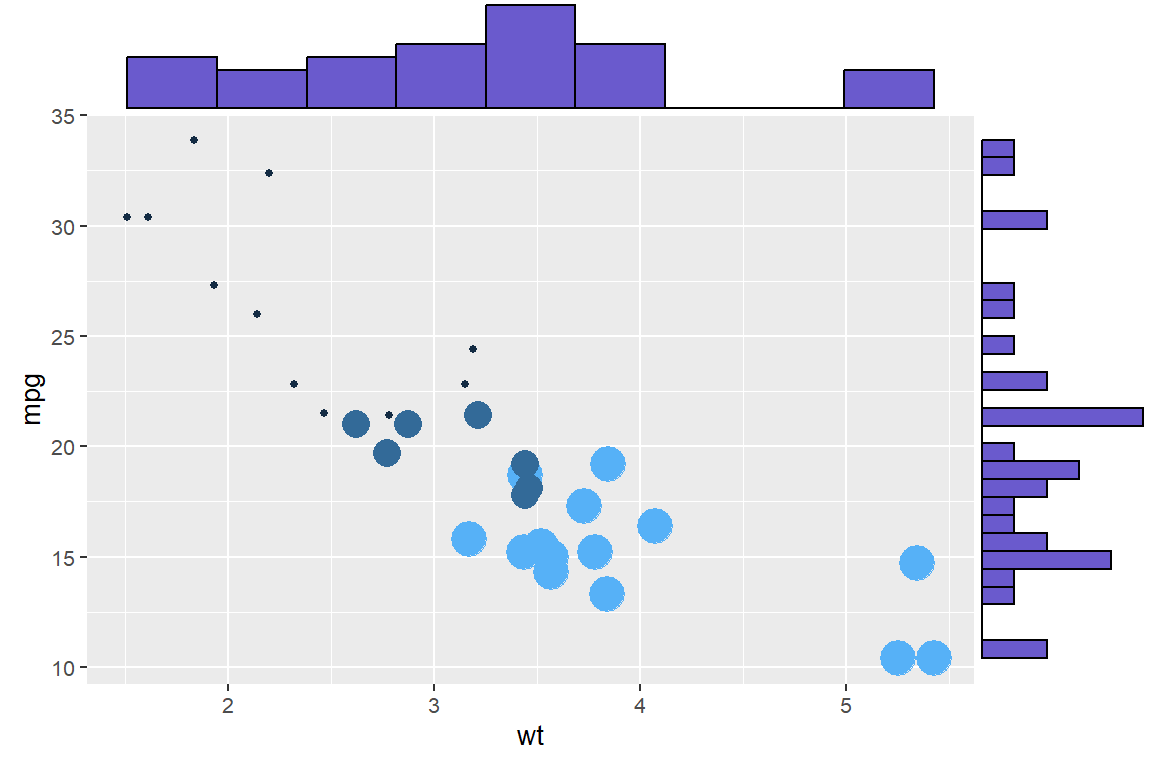
Source: Data extracted from the 1974 Motor Trend magazine and published by HENDERSON; VELLEMAN (1981). Visualization by HOLTZ ([s.d.]), available at The R Graph Gallery.

Figure 1.3: Relation between weight (1000lbs) (\(\text{wt}\)) and miles per galon (\(\text{mpg}\)) for combustion engine vehicles